Reverse Engineering example 2

Suppose to have an old vertical declining dial with italic hours.

Starting from an arbitrary cartesian reference system (horizontal x axis positive to the right, vertical y axis positive down) we take the following measurements:

crossing point between the equinox line and the 17 hour line : x=92.3 , y=82.3

crossing point between the equinox line and the 19 hour line : x=121.8 , y=64.7

crossing point between the equinox line and the 21 hour line : x=137.9 , y=55.1

Let's found the original design parameters of the dial.

1. Define a new vertical dial in File -> Parameters -> Type.

Do not care on dial parameters, the only purpose is to define the type of dial you are dealing with : horizontal, vertical, inclined etc. (only horizontal, vertical and inclined dials can now be managed by the reverse engineering tool).

2. In the same window set "Time zone displayed" to "true local" so that the longitude of the place will not be considered in the problem.

3. Check the "measured points" box in the Options window so that the input points will be drawn on the dial.

Uncheck all the day lines boxes except for the equinox line.

Uncheck "french hours" and check "italic hours".

Uncheck the "hour lines over the horizon only" box.

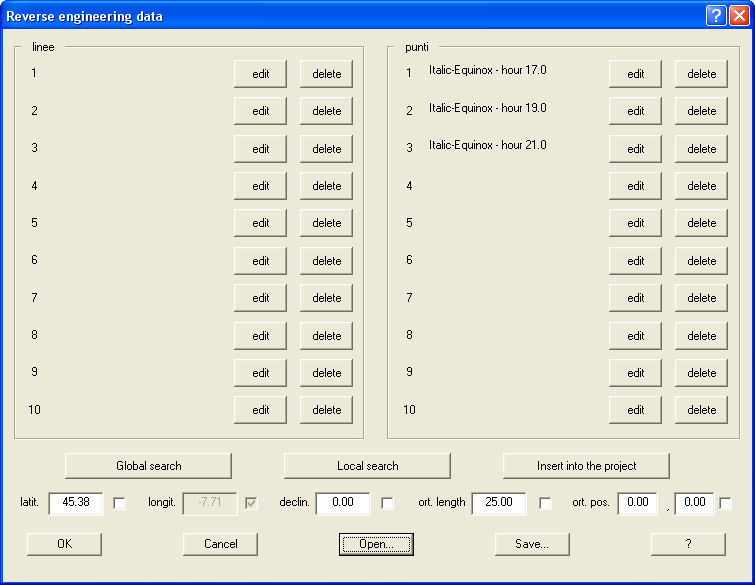
4. Open the Tools -> Reverse engineering window and introduce the three measured points.

The Reverse engineering window will look like the following one :

5. Now click the OK button, you will see the following graph :

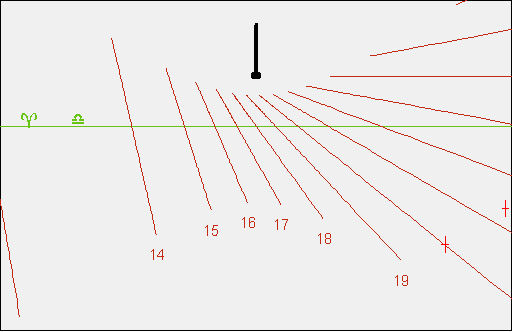
Here you can see the points you have just defined (only two are actually visible at the right of the dial). Italic hour lines are drawn but they are still erroneous of course.

6. Now in the Tools -> Reverse Engineering window click the Global search button.

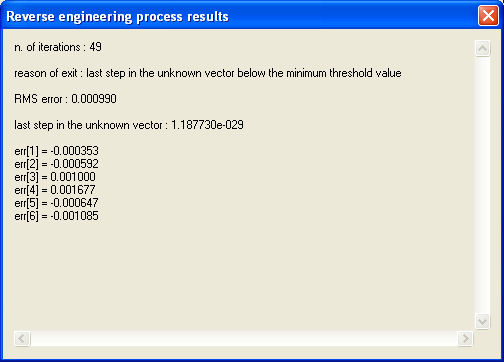
After a few seconds the following window will be displayed :

This message says that after 49 iterations the algorithm stopped because the last step was below the threshold, the RMS final error is 0.00099, the last step in the solution vector was 1.18e-29 and the residual error in the 4 equations is less than 0.002.

Now close the window.

The latitude, declination, ort. pos. x and y fields contain the result to the problem : 40.01, 30.05, 24.98 , 125.06 and 37.01 (input data have been obtained with lat=40 , decl=30 and style=25) .

8. Click the "Insert into the project" and then the "OK" button.

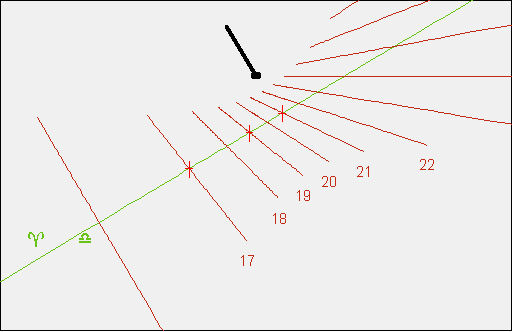
The following graph will be displayed, showing the resulting dial together with the input data.

aggiornato il venerdì 06 marzo 2015