Supponete di avere un antico quadrante verticale declinante ad ore italiche.

Stabilito un sistema di riferimento cartesiano arbitrario (asse x orizzontale positivo verso destra ed asse y verticale positivo verso il basso) misuriamo le seguenti coordinate :

incrocio tra linea equinoziale e linea oraria 17 : x=92.3 , y=82.3

incrocio tra linea equinoziale e linea oraria 19 : x=121.8 , y=64.7

incrocio tra linea equinoziale e linea oraria 21 : x=137.9 , y=55.1

Cerchiamo ora i parametri costruttivi originali del quadrante.

1. Definite un nuovo orologio verticale in File -> Parametri -> Tipo.

Non curatevi degli altri parametri dell'orologio, il solo scopo è quello di definire il tipo di quadrante con cui si ha a che fare : orizzontale. verticale, inclinato ecc. (per ora solo i quadranti orizzontali, verticali ed inclinati sono gestiti dal "Progetto inverso").

2. Nella stessa finestra impostate "ora visualizzata" su "vera locale" in modo che la longitudine del luogo non venga presa in considerazione nella soluzione del problema (in realtà il programma, avendo in input solo dati indipendenti dalla longitudine, non la prenderebbe comunque in considerazione).

3. Selezionate la casella "punti misurati" in Opzioni in modo che i dati di input vengano disegnati sul grafico del quadrante.

   De-selezionate tutte le caselle delle linee diurne, in quanto non ci interessano, e la casella "solo linee illuminate".

Deselezionate "ore francesi" e selezionate "ore italiche".

4. Aprite la finestra Strumenti -> Progetto inverso ed introducete i tre punti misurati.

La finestra apparirà come la seguente :

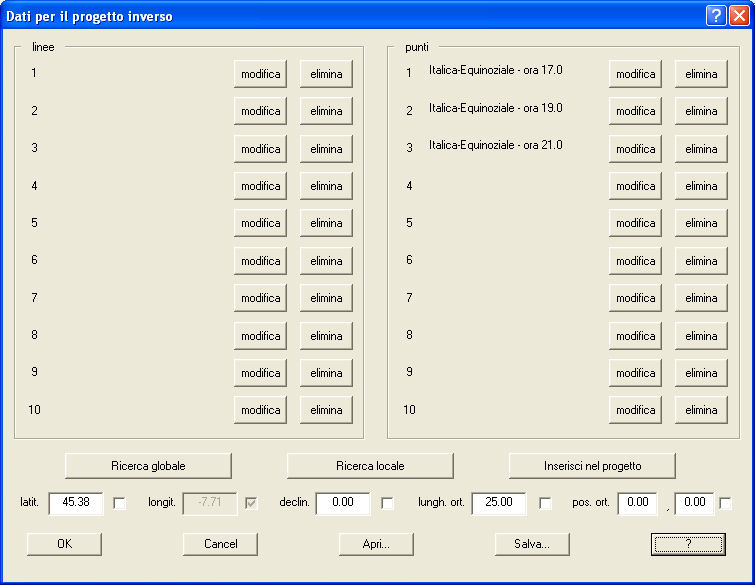
5. Ora cliccate il pulsanteOK ed il grafico diventerà il seguente :

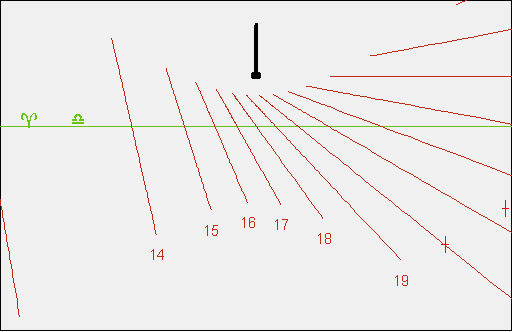
All'estrema destra in basso si vedono due dei tre punti introdotti. Le ore italiche rappresentate sono ovviamente ancora errate.

6. Ora nella finestra Strumenti -> Progetto inverso cliccate il pulsante Ricerca globale.

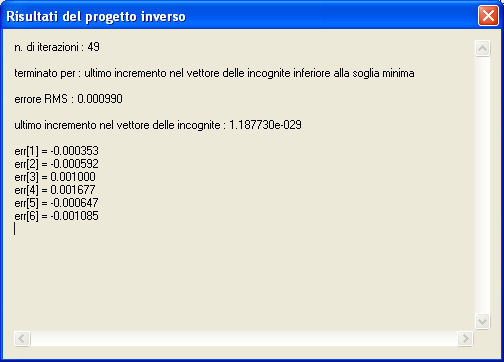
Dopo alcuni secondi apparirà la finestra seguente :

Questo messaggio vi dice che dopo un totale di 49 iterazioni l'algoritmo si è fermato perché l'ultimo passo nel vettore delle soluzioni era al di sotto della soglia, l'errore RMS finale è 0.00099, l'ultimo passo nel vettore della soluzione è stato 1.18e-29 e l'errore residuo nelle 4 equazioni è minore di 0.002

Chiudete la finestra.

I campi latitudine, declinazione, pos. ort. x e y contengono la soluzione al problema  : 40.01, 30.05, 24.98 , 125.06 e 37.01 (i dati di ingresso sono stati calcolati con lat=40 , decl=30 e stilo=25).

8. Cliccate "Inserisci nel progetto" e quindi "OK".

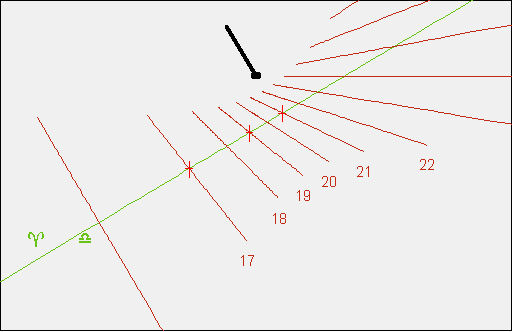
Il grafico rappresenta ora il quadrante risultante e, sovrapposti a questo, i punti di input al problema.

aggiornato il venerdì 06 marzo 2015